안녕하세요. 수학점수 올리는 명중샘입니다.
유튜브에서 보고 오셨다면, 잘 찾아오셨습니다~
여기 맞아요!
문제pdf 파일은 위 첨부파일 다운로드 받으세요!
위 첨부파일은 학습의 편의를 위해 유형/단원별 오름차순으로 재배열하였습니다.
Q. 명중샘 강의는 어디서 듣나요?
A. 유튜브에 "명중수학"을 검색하여, 구독/알람설정 등을 하면 훨씬 빠르게 들을 수 있어요. 또는 아래 링크로!
명중수학
초중고 수학강의 25년 경력 서울시 서대문구 남가좌동, 명중수학특목대입학원
www.youtube.com
블로그는 유튜브에 영상이 올라간 후 나중에 다시 이곳으로 정리하여 올려야하니 꽤 오래걸려요~
단, 유튜브에는 PDF 파일 등을 올릴 수가 없어서, 문제지/학습지는 계속하여 네이버 블로그에서 다운받으세요!
Q. 명중샘 강의는 어떻게 들으면 좋을까요?~
A.
상위권이라면,
수학은 실전이다! 쉬운문제부터 다풀고, 킬러문항 집중공략!
- 어려워 못푼문항 > 시간내에 못푼문항> 실수로 틀린문항 모두 복습하라!
1.시간(100분)을 재어 1번~30번까지 모두 푼다
2.채점 후, 오답문항만 명중샘 강의를 듣고 이해한다.
3.이해했다면, 강의를 멈춘후, 그 자리에서 스스로 다시 푼다.
4.막히면 다시 강의로! 풀리면 통과!
5.오답문항은 따로 모아 복습(반복풀이/다른풀이/빠른풀이 연구)한다!
중위권이라면,
단원별로 완전학습!! 단원이 끝나면 그 단원의 수능형 모의고사를 도전해보세요!
- 나중에는 30문항 100분내에 도전해보세요!
1.단원별로 모아 끊어서 푼다. (보통 6~8문항씩 배정)
2.채점후, 오답문항만 명중샘 강의를 듣고 이해한다.
3.이해했다면, 강의를 멈춘후, 그 자리에서 스스로 다시 푼다.
4.막히면 다시 강의로! 풀리면 통과!
5.다음 대단원도 위와 같이
하위권이라면,
천리길도 한걸음부터 한문항 한문항 정복하세요!
- 출발은 다르지만, 결국 수학은 누구나 1등급
1.1번 문항부터 차분히 읽고 미리 풀어본다.
2.명중샘 강의를 한문항씩 듣는다. 명중샘 풀이와 내 풀이가 같다면, 통과
3.명중샘 풀이와 내 풀이가 다르면, 비교해보고, 명중샘 풀이로도 다시 풀어본다.
4.오답문항은 확실히 이해를 한 후, 스스로 다시 풀어본다.
5.그 다음 문제로 넘어간다.
그 후, 중위권 방식으로 도전, 나중에는 상위권 방식으로 도전!
모의고사는 4~10년치 다섯 바퀴이상 돌려주면, 모두 1등급! 만점이예요!
참고, 모의 해설 강의는 명중샘이 실제 시험을 본다면! 이라는 가정으로 영상을 만들었어요.
가급적 실전풀이, 빠른 풀이로 제공하여 학생들이 100분이라는 시간내에 풀 수 있게하자는 목적을 가지고 있어요.
그러다보니, 공식이나 개념설명이 자세하지 못해서, 영상을 만든 명중샘도 많이 아쉬워요.
나중에는 문항의 구조적 분석! 문제 독해와 유형 분석, 필요한 공식과 개념 정리를 따로 만들어서 더 잘 이해할 수 있게 노력할게요! 화이팅!
- 수학점수 올리는 명중샘
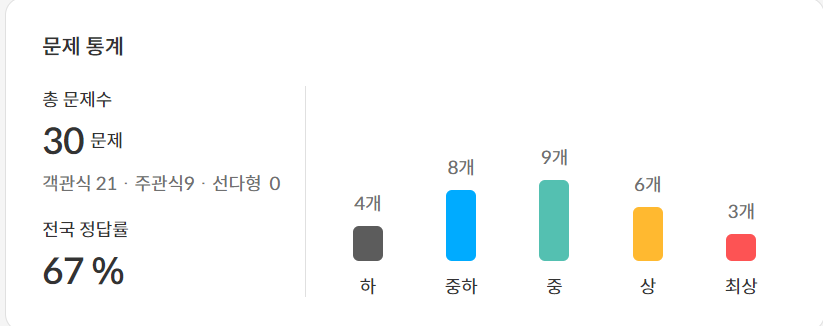
다음은 이번 모의고사 30문항에 대한, 전국 정답율과 문항 난이도, 문항별 유형분석 표입니다.
위 교재 PDF에 30문항은 아래 유형/단원 오름차순으로 정리 되어있습니다.


자, 그럼 지금부터 2022년 6월 고1 수학 모의 1번 ~ 30번 강의 시작! 합니다
(위 교재 PDF 순으로 - 유형/단원 오름차순)


'유튜브 명중수학' 카테고리의 다른 글
| 수학명언 "이 문제에 대한 나의 증명은 이 여백에 너무 좁아 적지 못 하겠다" 페르마의 생애와 업적 (0) | 2024.08.05 |
|---|---|
| 수학명언-아폴로니우스의 생애와 업적 (0) | 2024.08.05 |
| 수학명언 "마음이란 이해할 수 없는 녀석" - 파스칼의 생애와 업적 (0) | 2024.08.05 |
| 역수의 합/차의 곱셈공식의 변형식 (0) | 2024.08.05 |
| 중3-1 제곱근에 의한 이차방정식의 풀이 (0) | 2024.08.05 |



